1 Introduction & Outline
1.1 What is game theory?
The study of mathematical models of conflict and cooperation between intelligent rational decision-makers
It is effectively a multi-objective optimization, where multiple loss functions need to be optimized. The algorithmic part means that there will be algorithms for finding concepts discussed.
1.2 Prisoner’s dilemma
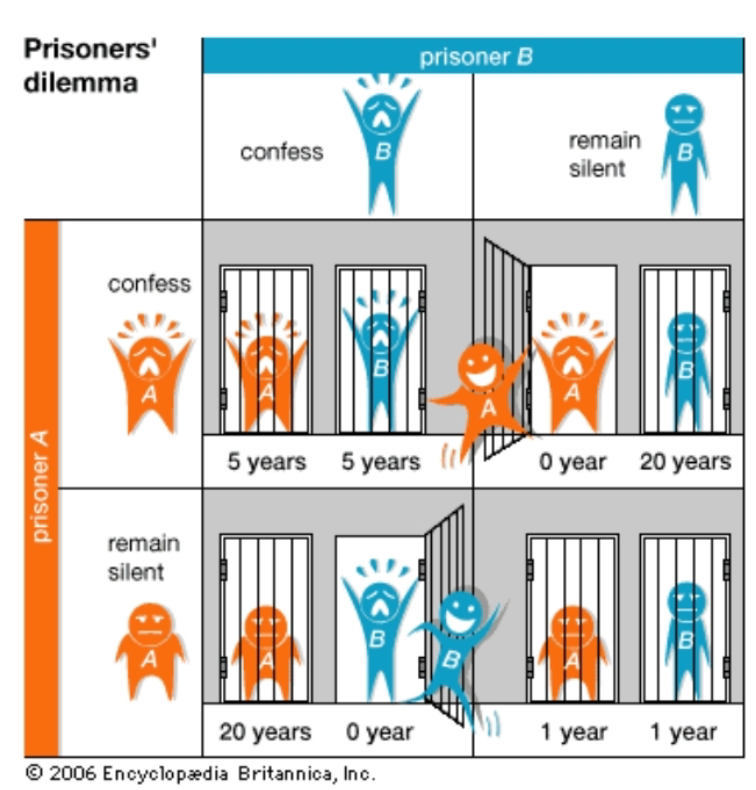
Two suspects of a serious crime are arrested and imprisoned. Police have enough evidence of only petty theft, and to nail the suspects for the serious crime they need testimony from at least one of them. The suspects are interrogated separately without any possibility of communication Each of the suspects is offered a deal:
- If he confesses (\(C\)) to the crime, he is free to go.
- The alternative is not to confess, that is remain silent (\(S\))
One prisoner is said to be a row player and the other is a column player and it following table there are payoffs row the row and column players.
| \(C\) | \(S\) | |
|---|---|---|
| \(C\) | \((-5,-5)\) | \((0,-20)\) |
| \(S\) | \((-20,0)\) | \((-1,-1)\) |
Rational “row” suspect (or his adviser) may reason as follows:
- If my colleague chooses \(C\), then playing C gives me −5 and playing \(S\) gives −20.
- If my colleague chooses \(S\), then playing C gives me 0 and playing \(S\) gives −1
In both cases, \(C\) is clearly better (it strictly dominates the other strategy). If the other suspect’s reasoning is the same, both choose C and get a 5-year sentence
There is a solution \((S, S)\) which is better for both players but needs some “central” authority to control the players
This suboptimality will be visible throughout the course.
1.3 Nash equilibria
1.3.1 Battle of Sexes
A couple agreed to meet this evening, but cannot recall if they will be attending the opera or a football match. One of them wants to go to the football game. The other one to the opera. Both would prefer to go to the same place rather than different ones.
Battle of Sexes can be modeled as a game of two players (the couple) with the following payoffs.
| \(O\) | \(F\) | |
|---|---|---|
| \(O\) | \((2,1)\) | \((0,0)\) |
| \(F\) | \((0,0)\) | \((1,2)\) |
Apparently, no strategy of any player is dominant. So what could be a “solution”? Note that whenever both players play \(O\), then neither of them wants to unilaterally deviate from his strategy! Here, \((O, O)\) is an example of a Nash equilibrium (as is \((F, F)\)).
This can be interpreted as advice to both players that they would have to deviate from.
The thinking process is the same as in physics. First, we make a model of a social situation then make a prediction and validate it.
1.3.2 Rock, Paper, Scissors
Again, the existence of a Nash equilibrium is not guaranteed - as can be seen in Rock, Paper, Scissors
| \(R\) | \(P\) | \(S\) | |
|---|---|---|---|
| \(R\) | \((0,0)\) | \((-1,1)\) | \((1,-1)\) |
| \(P\) | \((1,-1)\) | \((0,0)\) | \((-1,1)\) |
| \(S\) | \((-1,1)\) | \((1,-1)\) | \((0,0)\) |
This game is a zero-sum game - whatever one player wins, the other one loses.
We can further generalize the players’ behavior of the game into mixed strategies: Each player plays each pure strategy with probability \(\frac 1 3\). The expected payoff of each player is 0 (even if one of the players changes his strategy, he still gets 0!).
It is always assumed that each player tries to maximize their payoff (they’re playing rationally).
1.4 Dynamic Games
So far we have seen games in strategic form that are unable to capture games that unfold over time (such as chess).
For such purpose, we need to use extensive form games. So it can be said that they are iterated or repeated games.
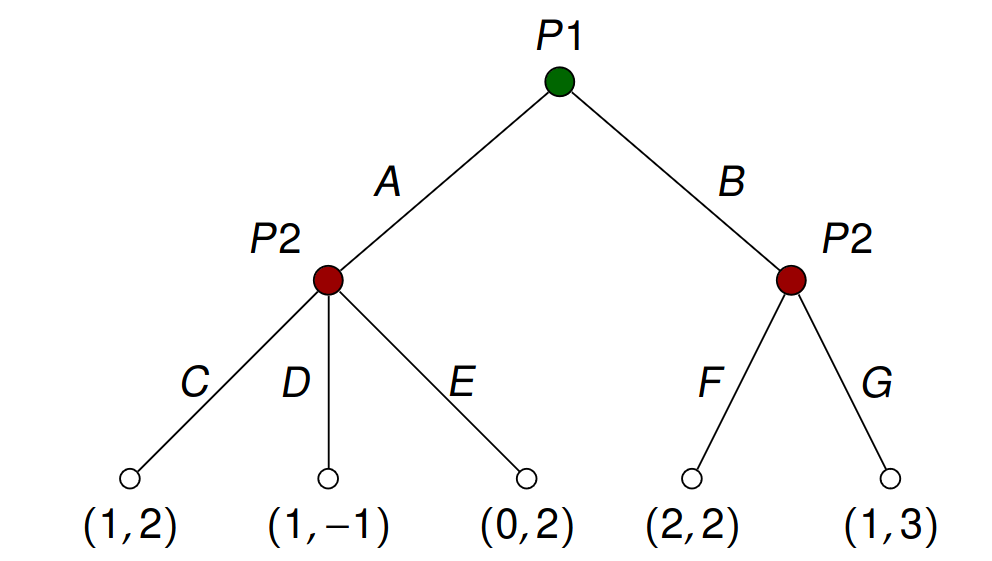
In this tree a player P1 chooses an action \(A\) or \(B\). Then the player P2 follows by choosing from actions \(C, D, E, F, G\).
1.4.1 Imperfect information
Some decisions in the game tree may happen by chance and are controlled by neither player (e.g. Poker, Backgammon, etc.)
Sometimes a player may not be able to distinguish between several “positions” because he does not know all the information in them (Think a card game with the opponent’s cards hidden). For this purpose, we will introduce so-called information sets (and these games are imperfect information games).
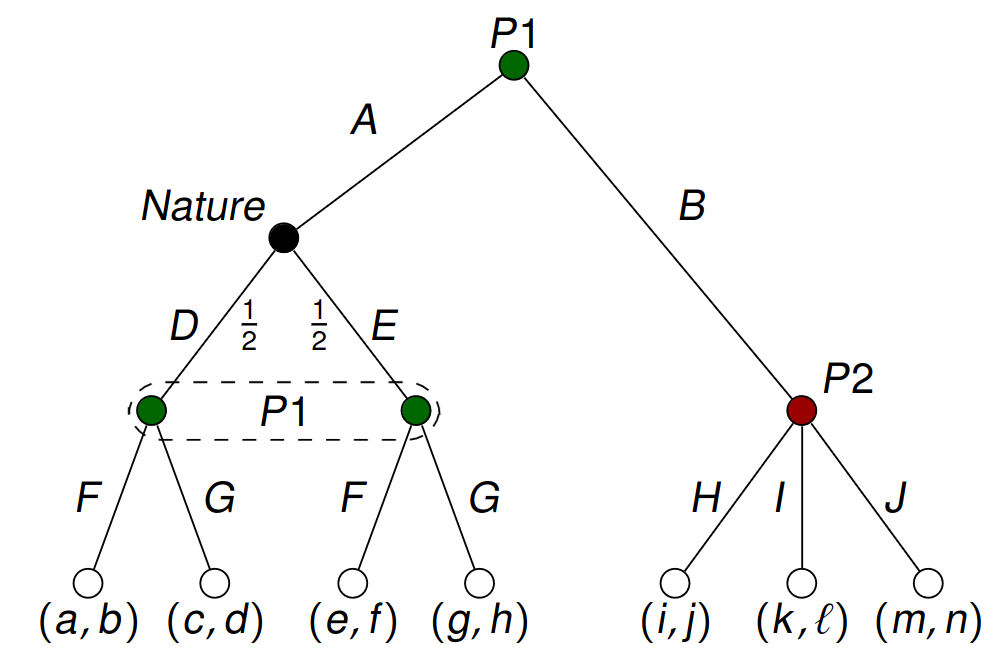
1.4.2 Incomplete information
In all previous games, the players knew all the details of the game they played, and this fact was a “common knowledge”. This is not always the case.
1.4.2.1 Sealed Bid Auction
Two bidders are trying to purchase the same item.
- The bidders simultaneously submit bids \(b_1\) and \(b_2\) and the item is sold to the highest bidder at his bid price (first price auction)
- The payoff of the player 1 (and similarly for player 2) is calculated by \[ u_1(b_1,b_2) = \begin{cases} v_1 - b_1 & b_1 > b_2 \\ \frac 1 2 (v_1 - b_1) & b_1 = b_2 \\ 0 & b_1 < b_2 \end{cases} \] Here \(v_1\) is the private value that player 1 assigns to the item and so player 2 does not know \(u_1\).
1.5 Inefficiency of Equilibria
In Prisoner’s Dilemma, the selfish behavior of suspects (the Nash equilibrium) results in a somewhat worse-than-ideal situation
Defining a welfare function \(W\) which to every pair of strategies assigns the sum of payoffs, we get \(W(C, C) = −10\) but \(W(S, S) = −2\).
Such choice of a welfare function is generally arbitrary, but results vary depending on this choice.
The ratio \(\frac {W(C,C)} {W(S,S)} = 5\) measures the inefficiency of “selfish-behavior” \((C, C)\) w.r.t. the optimal “centralized” solution. Price of Anarchy is the maximum ratio between values of equilibria and the value of an optimal solution.
1.5.1 Selfish routing
Consider a transportation system where many agents are trying to get from some initial location to a destination. Consider the welfare to be the average time for an agent to reach the destination.
There are two versions:
- “Centralized”: A central authority tells each agent where to go.
- “Decentralized”: Each agent selfishly minimizes his travel time.
Price of Anarchy measures the ratio between average travel time in these two cases.
Problem: Bound the price of anarchy over all possible routing games?
1.6 Games in Computer Science
Game theory is a core foundation of mathematical economics. But what does it have to do with CS?
- Games in AI: modeling of “rational” agents and their interactions.
- Games in machine learning: Generative adversarial networks (GANs), reinforcement learning
- Games in Algorithms: several game theoretic problems have a very interesting algorithmic status and are solved by interesting algorithms
- Games in modeling and analysis of reactive systems: program inputs viewed “adversarially”, bisimulation games (the tester is trying to kill the program by weird inputs), etc.
- Games in computational complexity: Many complexity classes are definable in terms of games: PSPACE, polynomial hierarchy, etc.
- Games in Logic: modal and temporal logics, Ehrenfeucht-Fraisse games, etc.